Deep Space Mission Design Laboratory　　ISAS/JAXA

English

川勝研究室 - Kawakatsu Lab -

研究分野

JAXA宇宙科学研究所に属する川勝研究室は宇宙機の運動を議論するアストロダイナミクス・軌道力学分野，とりわけ深宇宙探査ミッションの軌道設計を中心に研究を行っています．深宇宙探査ミッションとは，地球を離れ，月や他の天体を探査する宇宙ミッションを指します．

探査機の軌道設計において基本となるのはニュートンの万有引力の法則です．特に太陽等の天体に対する探査機の力学は，二体問題で記述することができ，軌道設計における基礎となります．

近年では，計算能力の向上やイオンエンジンの登場といった科学技術の発展に伴いより高度な軌道設計が可能となり，二体問題の枠組みを超えた軌道設計に関する研究が盛んに行われています．スイングバイや三体問題の利用，そしてイオンエンジン等の低推力推進を利用した軌道設計により，小さなエネルギーで目標へ到達することができるようになります．川勝研究室では，それらのテーマを中心に研究を行っています．以下ではいくつかの研究内容を紹介します．

スイングバイ

軌道部品接続法 +

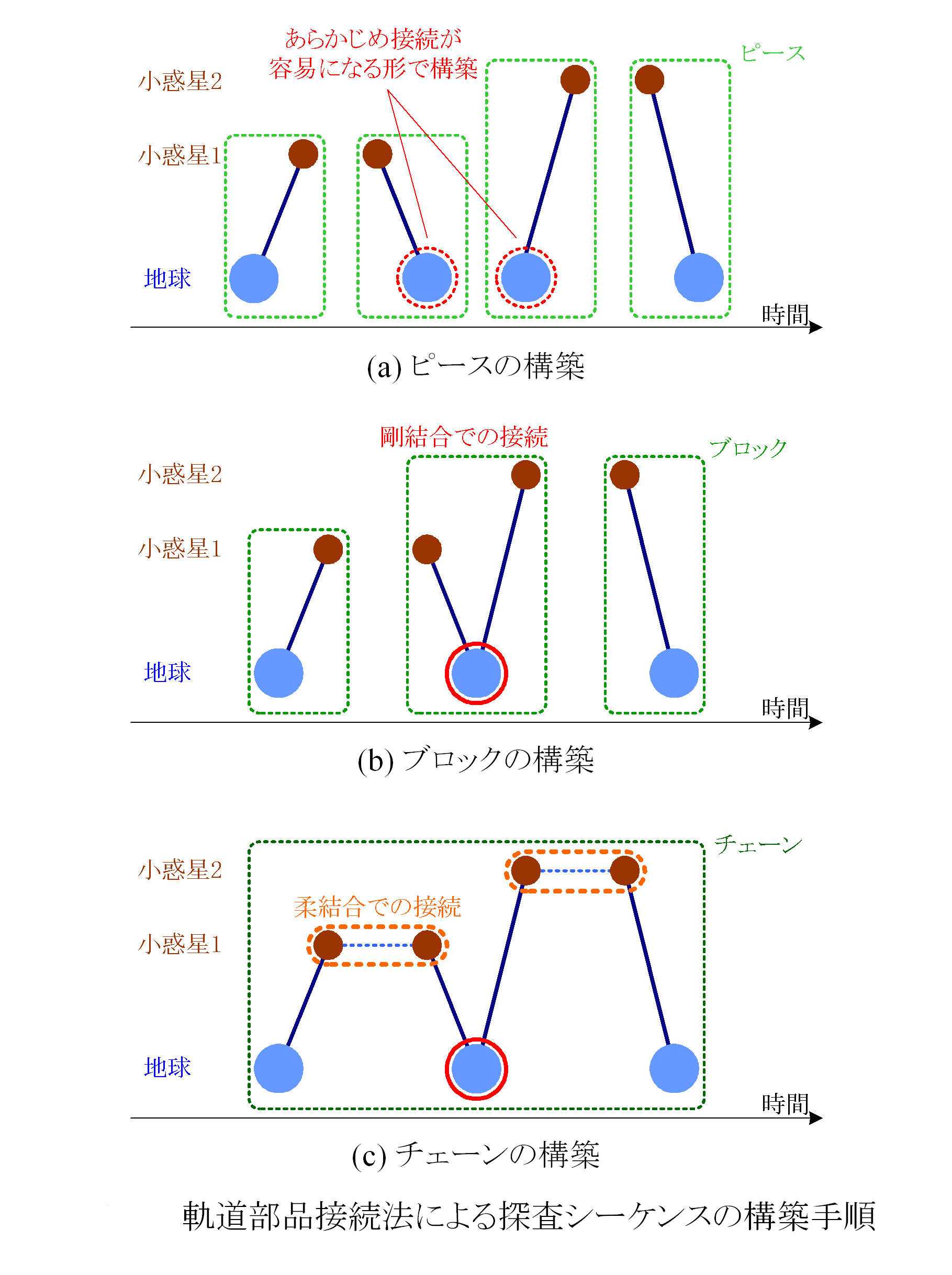
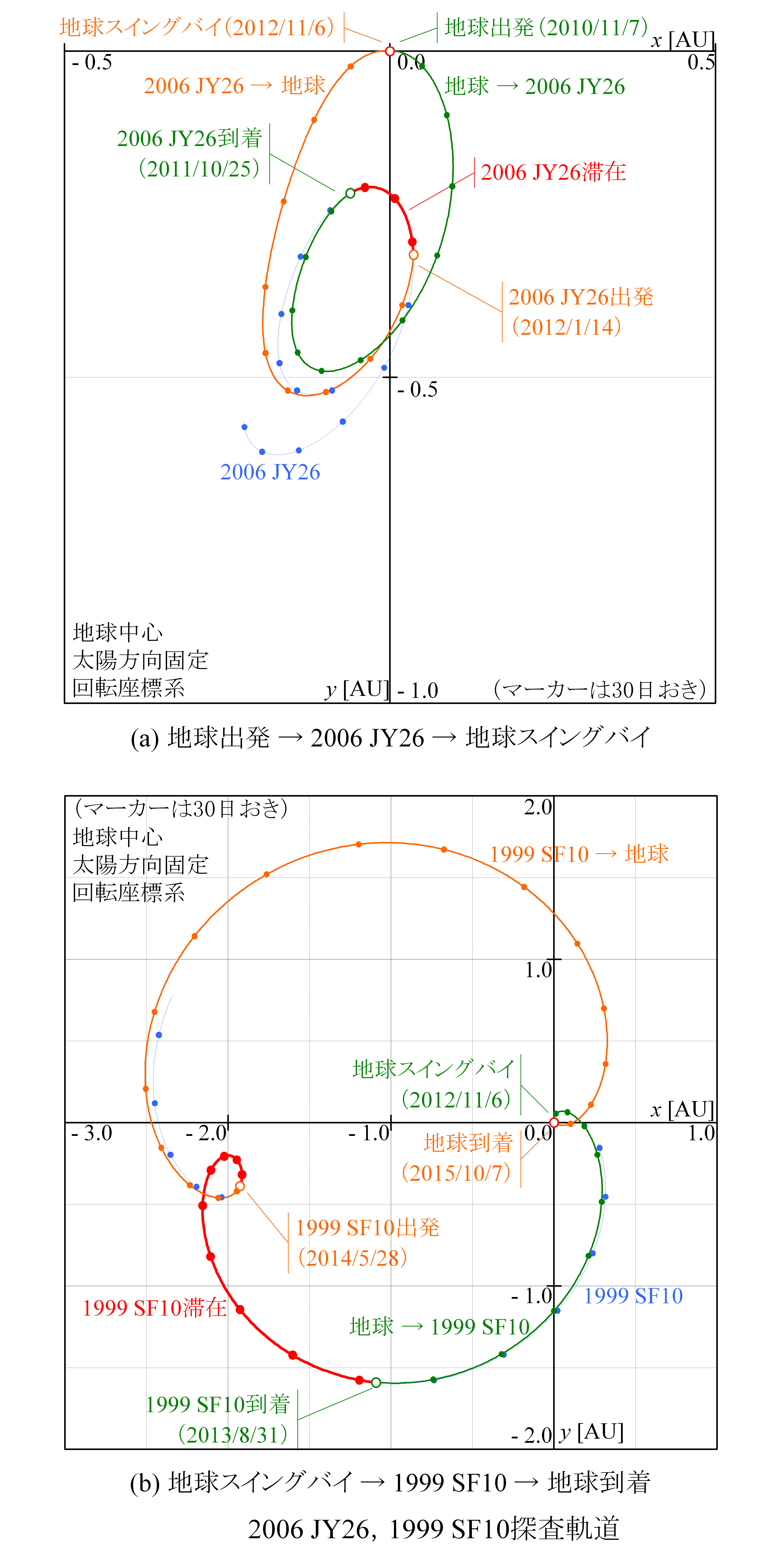
軌道部品接続法はスイングバイを介した惑星間軌道を効率的に，かつ網羅的に構築するために開発された手法です．事前に，天体へのスイングバイ・ランデブーといったイベントを両端(ノード)として構成した軌道群(ピース)を用意しておき，それらを接続していくことで複雑な軌道シーケンスを容易に構築することが可能となります．

本手法を用いることにより複数小天体からのサンプルリターン計画の検討，金星・地球スイングバイの体系的解析，地球圏脱出軌道の検討等が行われています．従来は二体モデルの下でピースの作成を行っていましたが，近年は三体モデルの下でピースを作成し地球圏内の低エネルギー遷移軌道構築への応用を考えています.

ロバスト軌道投入 +

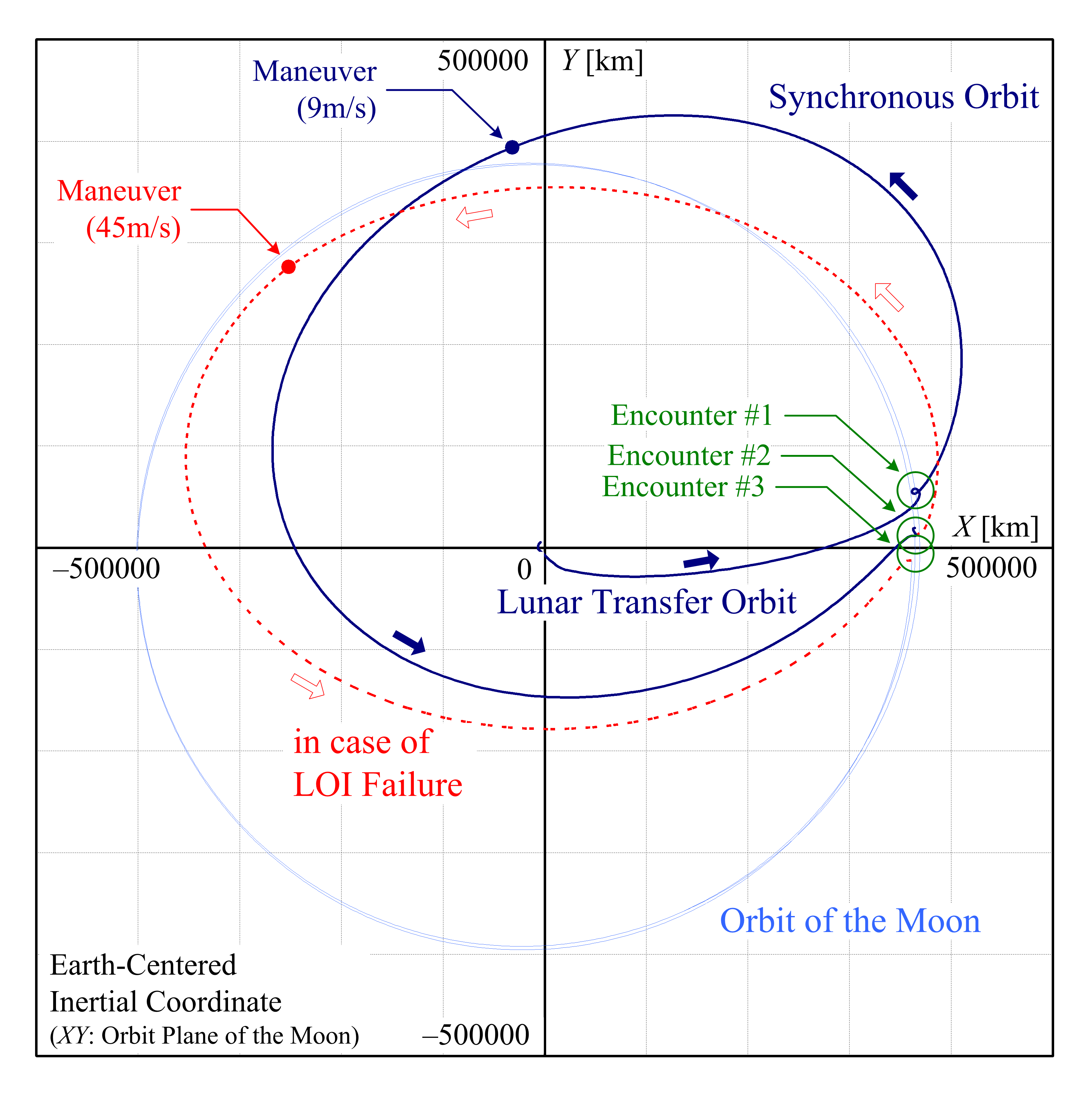
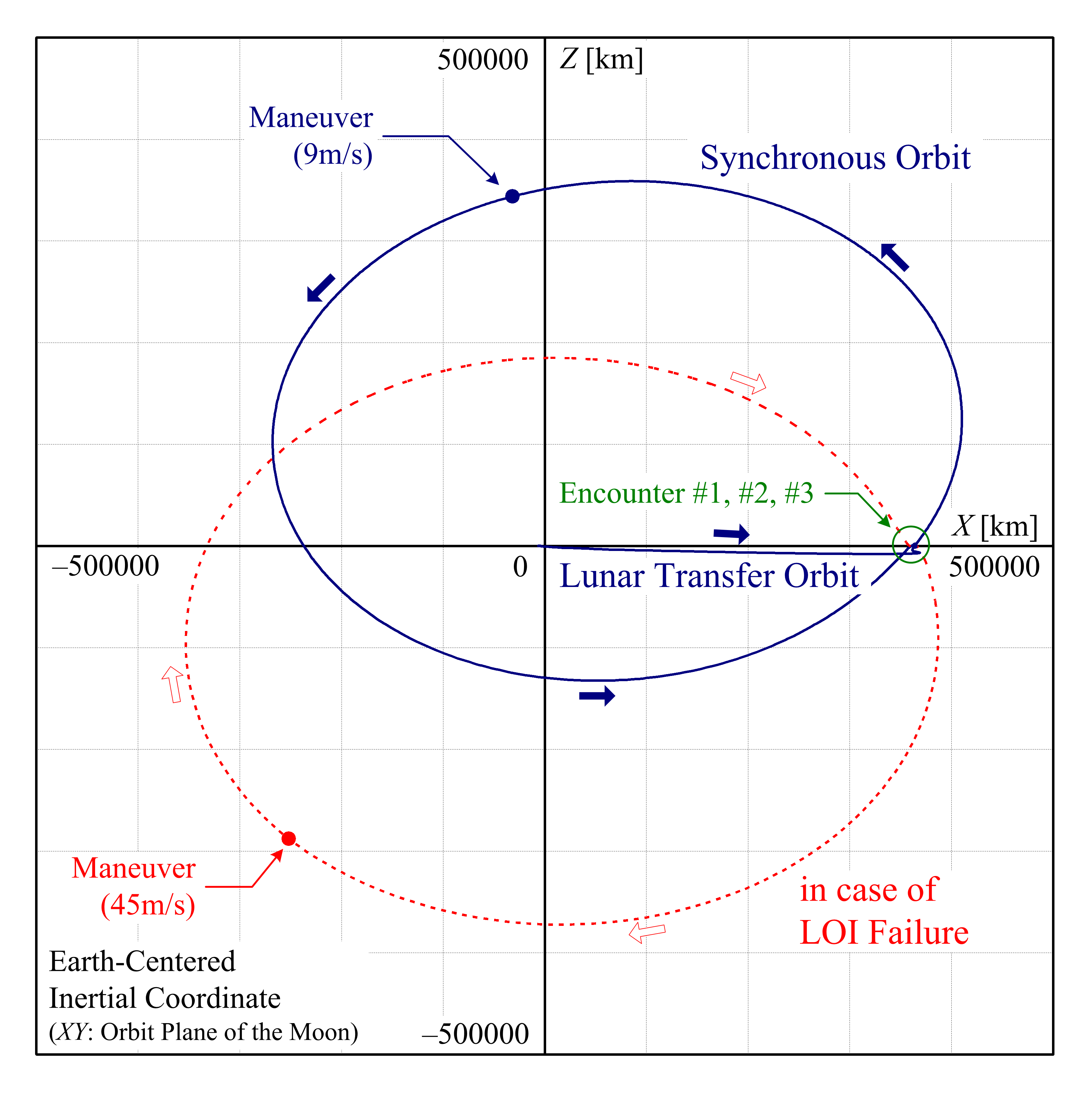
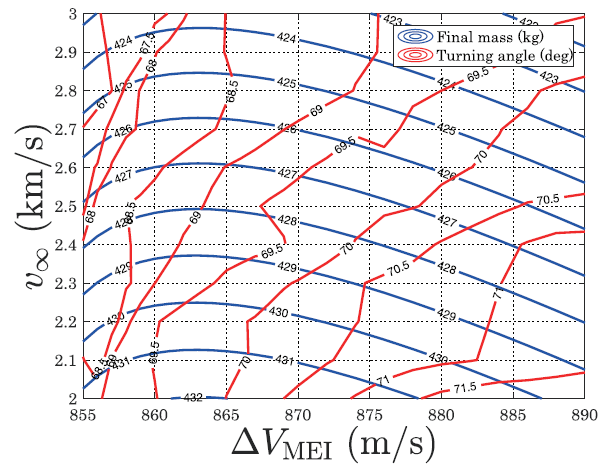
惑星探査ミッションにおいて，周回軌道投入は最もクリティカルなイベントです．何かしらのアクシデントにより軌道投入に失敗した場合でも軌道投入のリトライができる軌道を予め設計しておくことで最終的な軌道投入失敗に対するリスクを最小化する事ができます．このような軌道の実現のためには条件の工夫が必要となり「ロバスト軌道投入」という新たな手法を開発しました．図では月周回軌道投入に適応した例を示しています．

本研究は現在計画されている火星衛星探査計画(MMX)における火星周回軌道投入で採用されようとしています．

ティスラン図と衛星ツアー +

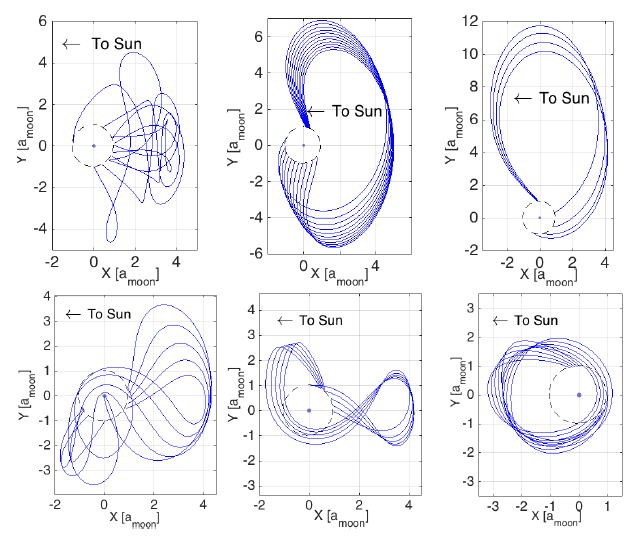
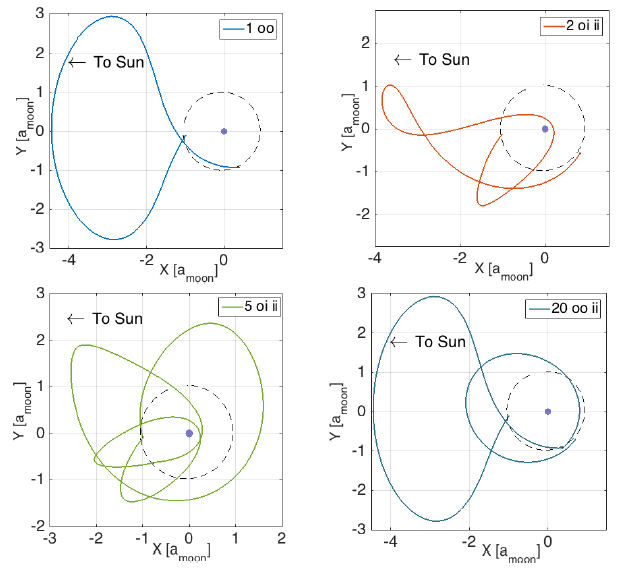
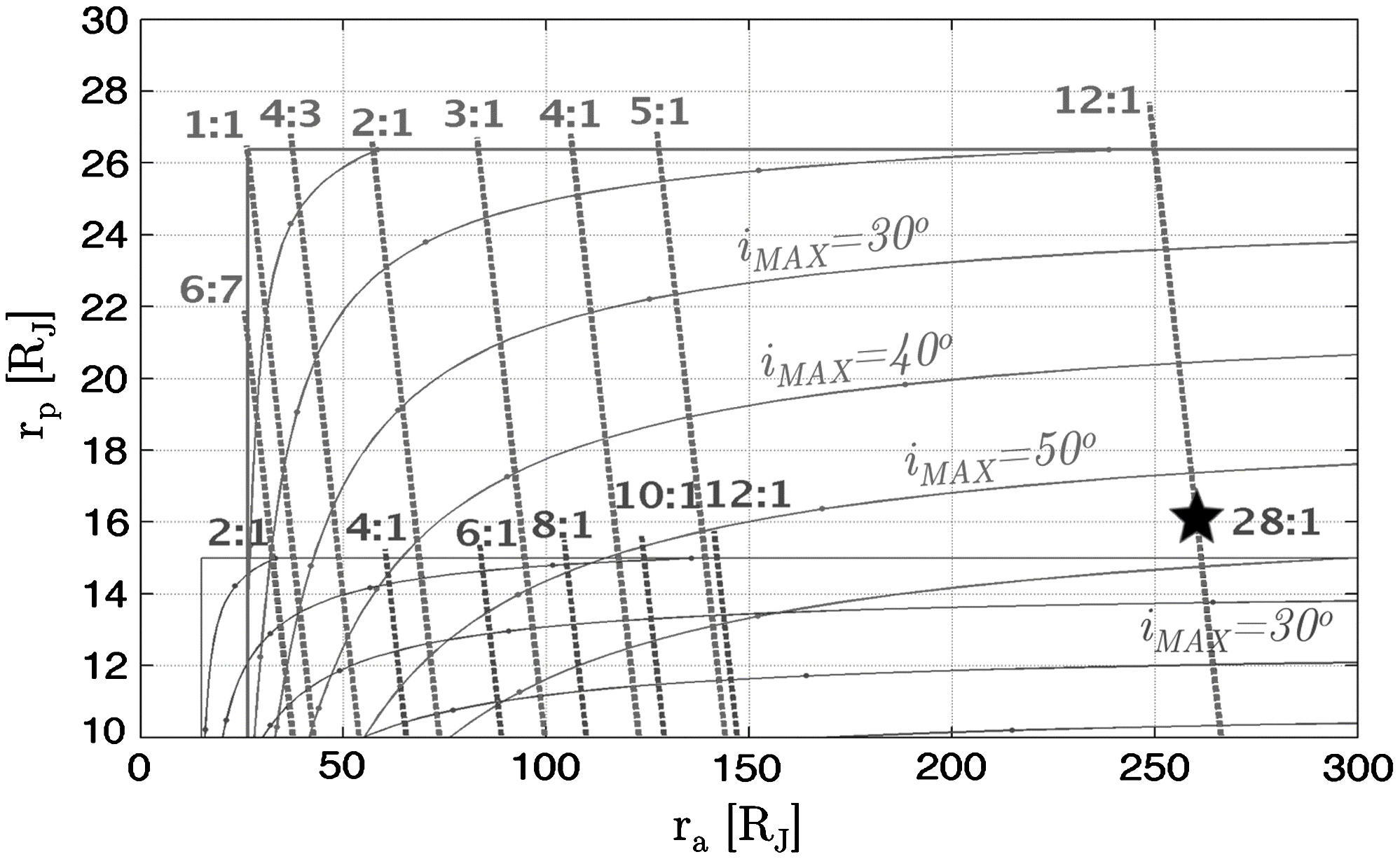
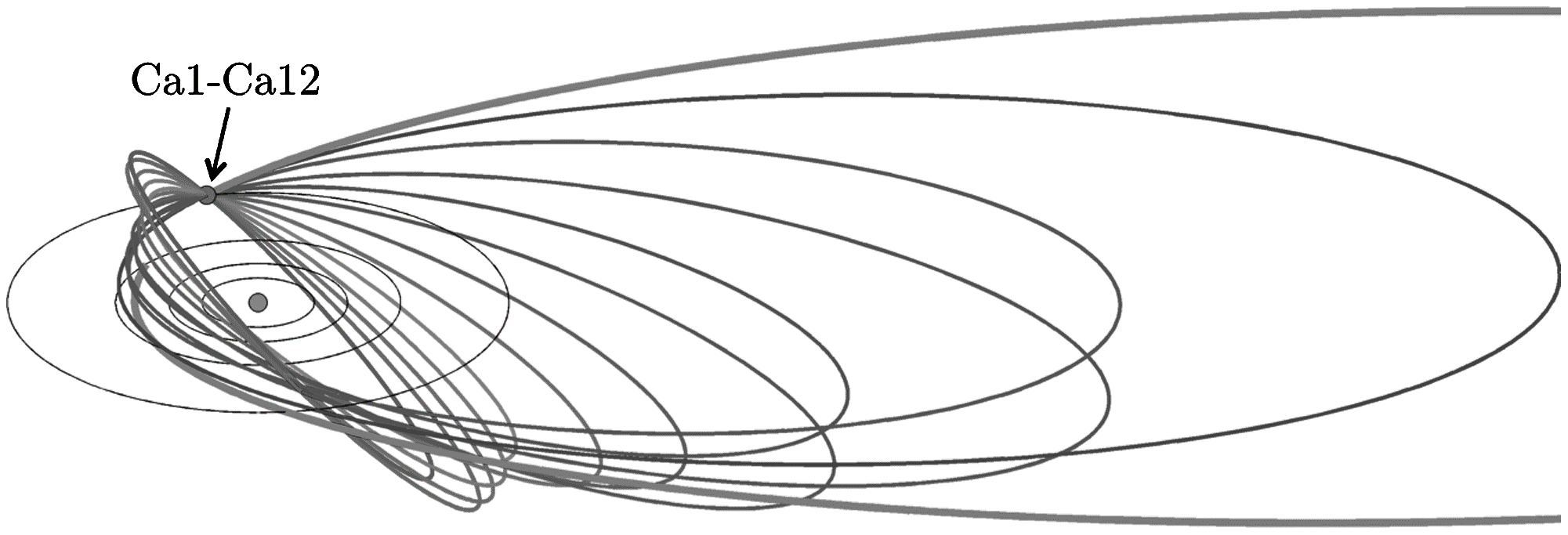
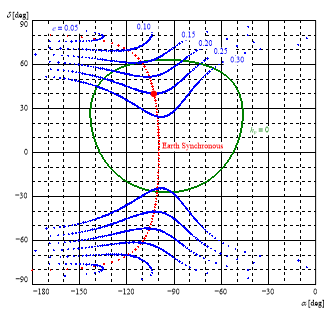
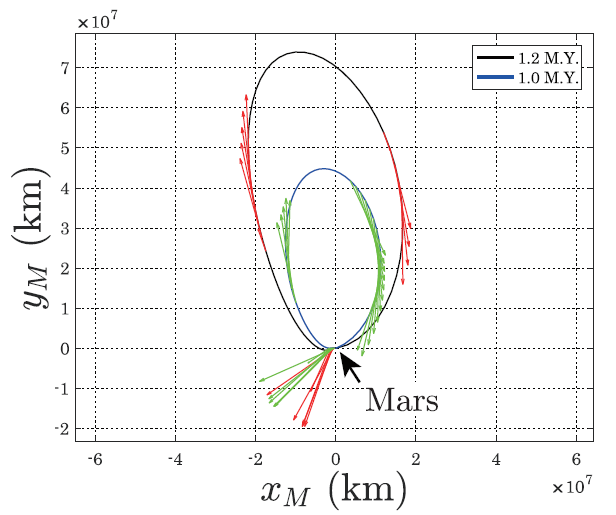
スイングバイ前後の軌道要素の間で保存される量として「ティスラン・パラメータ」があります．このティスラン・パラメータを元にスイングバイの力学的構造を捉えたティスラン図(左図)を提案し，木星等の惑星系においてマルチ・スイングバイを行う衛星ツアーの軌道計画において有効なツールとなっています．右の図はマルチ・スイングバイを行うことで軌道傾斜角を変化させている様子を示しています．

現在は地球圏内の低エネルギー遷移軌道における多重月スイングバイ・シーケンスに適応させるための拡張を進めています．

低推力推進

シーケンシャルEDVEGA +

EDVEGA(Electric Delta-V Earth Gravity Assist)は電気推進系と地球スイングバイを用いる手法であり，世界で初めて適用されたのが「はやぶさ」の軌道です．このEDVEGAを多段階的に用いる手法をシーケンシャルEDVEGAと呼びます．EDVEGAでは地球同期軌道上を電気推進を用いながら飛行し，約一年ごとに地球と会合します．会合時に地球スイングバイを用い，大きな軌道制御を行います．

スパイラル軌道 +

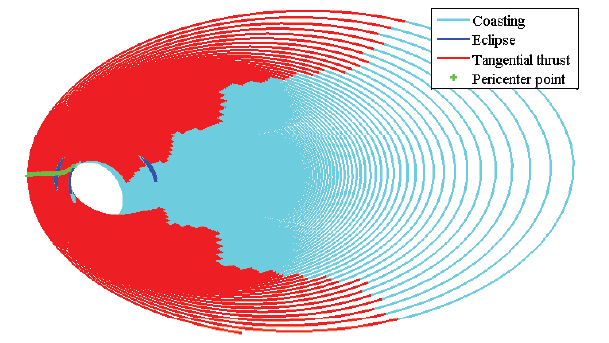
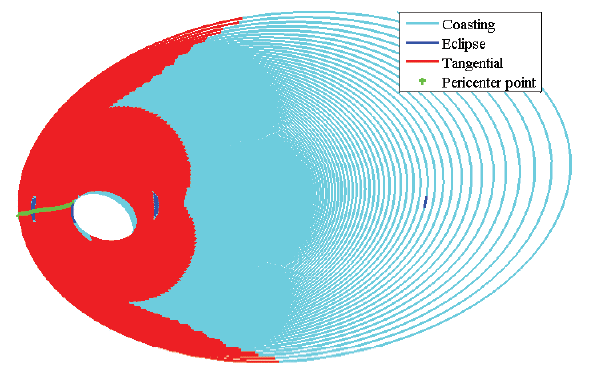
惑星周回軌道において，低推力推進により徐々に軌道を変更していく軌道操作手法である「スパイラル軌道」に関する研究で軌道遷移や静止衛星への応用が考えられています．スパイラル軌道は惑星周りを数百周するといった特徴があり，軌道伝播や軌道設計には高度な手法を用いる必要があります．特に様々な目的関数を扱ったの体系的設計手法の確立は大きな課題となっています．

そこで，遺伝的アルゴリズムを用いた多目的最適化を行うことによりパレート面を形成し設計解群を求めます．これらは深宇宙探査技術実証機DESTINY⁺のスパイラル軌道設計に応用されています．左の図ではイオンエンジン噴射時間最小ケースを，右の図では放射線通過時間最小ケースを示しており，目的によって軌道が変化していることが確認できます．

三体モデル下の電気推進軌道設計 +

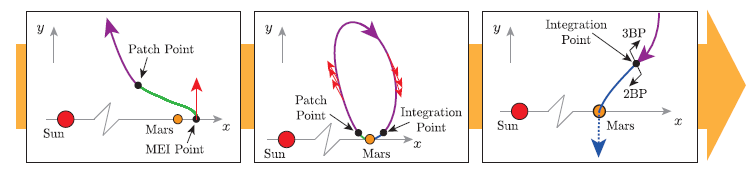
三体モデルとして取り扱う必要性のある領域において電気推進を用いた軌道設計は難易度が高いものとなっています．これは保存量が多数存在する二体モデルに対して，三体モデルには保存量が一つしか存在しないためです．そこで惑星近傍を並走する軌道を用いることで三体モデル下の設計手法を確立しました．

この手法は火星衛星探査計画(MMX)の復路軌道のオプション検討に適応されています．

三体問題

ハロー軌道と力学系理論 +

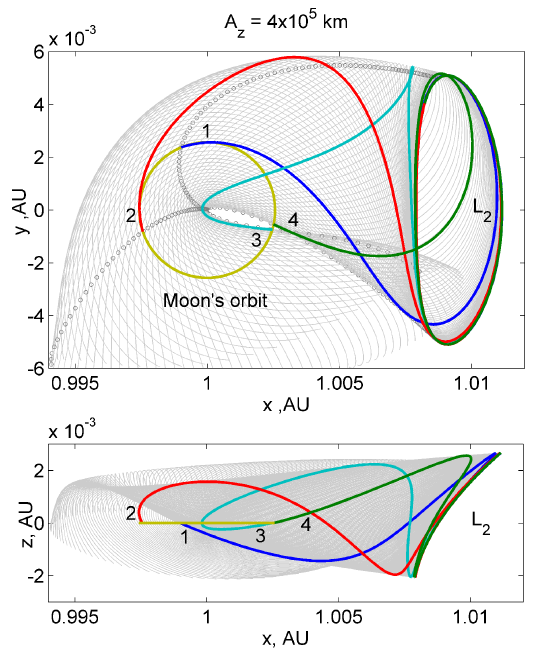
ハロー軌道は制限三体問題の平衡点近傍を周回する周期軌道のことです．ハロー軌道は観測衛星や宇宙港などで利用が考えられており，性質を把握することは重要な課題です．

ハロー軌道の安定性解析や遷移軌道を求めるために力学系理論を用いています．

ハロー遷移軌道と月スイングバイ +

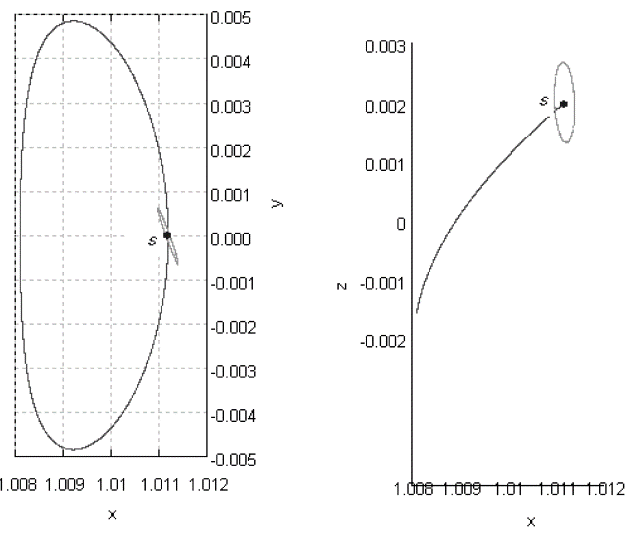
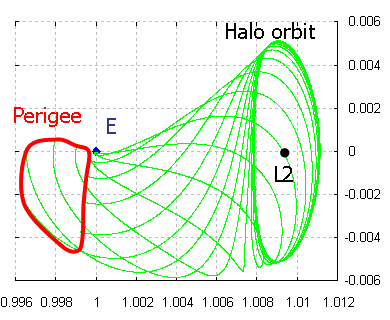
ハロー軌道の安定多様体と不安定多様体を月と接続することで月スイングバイの利用とハロー軌道を結びつけることができます．前者の場合ハロー軌道投入に月スイングバイを利用でき，後者の場合はハロー軌道を出発した探査機が月スイングバイを利用することが可能となります．

月スイングバイを利用することで，より低エネルギーでのハロー軌道遷移や地球圏脱出を行うことができるため小型探査機での応用が検討されています．

地球圏内の低エネルギー遷移軌道 +

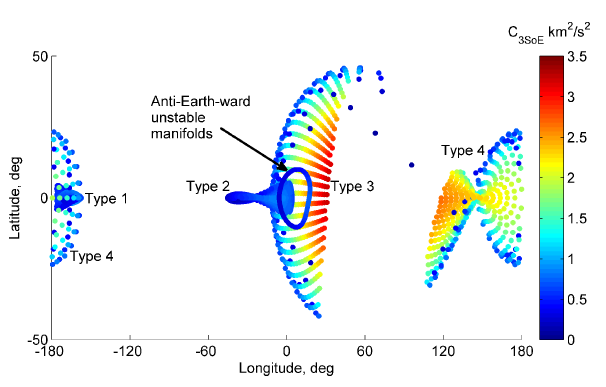
地球圏内において月スイングバイなどを駆使することで少ない軌道制御量で目標の軌道を達成する事ができます．このような軌道を低エネルギー遷移軌道と呼び，搭載燃料の限られる小型探査機の実現の一助となるため注目が集まっています．

月スイングバイを複数回用いることから，低エネルギー遷移軌道の軌道設計は複雑であり，体系的な設計手法の構築が求められています．

最近の主な論文・発表

学術論文 (Selected)

• Hongru Chen, Yasuhiro Kawakatsu and Toshiya Hanada, "Phasing Delta-V for transfers from Sun-Earth halo orbits to the Moon", Acta Astronautica, Vol. 127, pp.464-473, 2016.
• Bruno Victorino Sarli,Kaito Ariu,Hajime Yano.” PROCYON’s probability analysis of accidental impact on Mars”,Advances in Space Research.Vol.57,pp2003,1 May,2015.
• Masaki Nakamiya, Yasuhiro Kawakatsu. "Transfer Trajectories from the Moon to Sun-Earth Halo Orbits" Journal of Guidance, Control and Dynamics. Vol. 37, No. 3, May-June 2014.
• Campagnola, S., Buffington, B. B., Petropoulos, A. E. , Jovian tour design for orbiter and lander missions to Europa. Acta Astronautica, 2014, Vol. 100, pp. 6881, DOI:10.1016/j.actaastro.2014.02.005.
• Campagnola, S., Boutonnet, A., Schoenmaekers, J., Grebow,D.J., Petropoulos, A. E., Russell, R. P., Tisserand-Leveraging Transfers, Journal of Guidance, Control, and Dynamics, Vol. 34, No. 4, pp. 12021210, 2014. DOI:10.2514/1.62369.
• Campagnola, S., Boutonnet, A., Martens, W., Masters, A. Mission design for the exploration of Neptune and Triton (IEEE Aerospace and Electronics Systems Magazine, in print.
• Masato Nakamura, Yasuhiro Kawakatsu, Chikako Hirose, Takeshi Imamura, Nobuaki Ishii, Takumi Abe, Atsushi Yamazaki, Manabu Yamada, Kazunori Ogohara, Kazunori Uemizu, Tetsuya Fukuhara, Shoko Ohtsuki, Takehiko Satoh, Makoto Suzuki, Munetaka Ueno, Junichi Nakatsuka, Naomoto Iwagami, Makoto Taguchi, Shigeto Watanabe, Yukihiro Takahashi, George L. Hashimoto, Hiroki Yamamoto. "Return to Venus of the Japanese Venus Climate Orbiter AKATSUKI" Acta Astronautica. 93 (2014) pp.384-389, 30 July, 2013.
• Sugimoto, Y. and Van der Ha, J.C., “Thermal Radiation Modeling for Interplanetary Spacecraft Orbit Propagation,” Transaction of the Japan Society for Aeronautical and Space Sciences, Aerospace Technology Japan, Vol. 10, No. ists28, pp. Pd 33-38, January 26, 2013
• Campagnola S., Russell R., Skerritt P., Flybys in the planar, circular, restricted, three-body problem, Celestial Mechanics and Dynamical Astronomy, Vol. 113, No. 3, pp. 343-368, 2012, DOI: 10.1007/s10569-012-9427-x.
• Campagnola, S. and Kawakatsu, Y.,Jupiter Magnetospheric Orbiter: Trajectory Design in the Jovian System, Journal of Spacecraft and Rockets, Vol. 49, No. 2, pp. 318-324, 2012, DOI: 10.2514/1.A32055.
• Campagnola, S. and Kawakatsu, Y., Three-Dimensional Resonant Hopping Strategies and the Jupiter Magnetospheric Orbiter, Journal of Guidance, Control, and Dynamics, Vol. 35, No. 1, January-February 2012, pp. 340-344, 2012, DOI: 10.2514/1.53334.

国際会議 (Selected)

• Shuntaro Suda,Yasuhiro Kawakatsu,"Orbit Manipulation by use of Lunar Swing-by on a Hyperbolic Trajectory",The 27th AAS/AIAA Space Flight Mechanics Meeting,San Antonio,USA,Feb 5-9,2017.
• Yosuke Kawabata,Yasuhiro Kawakatsu,"Mission design of DESTINY+",67th International Astronautical Congress,Mexicanos,Sep 26-30,2016.
• Makoto Horikawa,Takanao Saiki,Yasuhiro Kawakatsu,Hiroaki Yoshimura,"Escape Trajectories for Martian Moons eXplorer using Chemical and Electric Propulsion",2016 AIAA/AAS Astrodynamics Specialist Conference,Long Beach,USA,Sep 12-15,2016.
• Hongru Chen, Yasuhiro Kawakatsu and Toshiya Hanada, "Earth Escape from a Sun-Earth Halo Orbit Using Unstable Manifolds and Lunar Gravity Assists", 25th Workshop on Astrodynamics and Flight Mechanics, ISAS/JAXA, Jul 28-29, 2015.
• Hongru Chen, Yasuhiro Kawakatsu and Toshiya Hanada, “Transfers from Sun-Earth Halo Orbits to the Moon”, 30th International Symposium on Space Technology and Science, Kobe , Hyogo, Japan, Jul 4-10, 2015.
• Hongru Chen, Yasuhiro Kawakatsu and Toshiya Hanada, "Phasing Problem for Sun-Earth Halo Orbit to Lunar Swingby Encounter Transfers", 25th AAS/AIAA Space Flight Mechanics Meeting, Williamsburg, VA, Jan 11-15, 2015.
• Yam, C. H., Sugimoto, Y., Ozaki, N., Sarli, B., Chen, H., Campagnola, S., Ogura, S., Kawabata, Y, Kawakatsu, Y., Nakajima, S., Funase, R., Nakasuka, S., "Launch Window and Sensitivity Analysis of an Asteroid Flyby Mission with Miniature Ion Propulsion System: PROCYON," 65th International Astronautical Congress, Toronto, Canada, Sep. 29-Oct. 3, 2014, IAC-14-C1.9.9.
• Yam, C. H., Zuiani, F., Kawakatsu, Y., Yamamoto, T., and Vasile, M., "Orbit Raising Trajectory and System Analysis for the Mission DESTINY," 24th International Symposium on Space Flight Dynamics, Maryland, U.S.A., May 5-9, 2014.
• Campagnola, S., Russell, R. Optimal control on Gauss' Equation (Proceedings of the 2nd DyCoSS conference, 2014).
• Yam, C. H., and Kawakatsu, Y., "High Fidelity Direct Transcription Method For Optimization Of Many Revolution, Low-thrust Trajectories," 2nd IAA Conference on Dynamics and Control of Space Systems, Rome, Italy, March 24-26, 2014.
• Ogura, S., Kawakatsu, Y. Matsuoka, A., Taguchi, M. "Visual Orbit Design for Next Mars Exploration Mission" 2nd IAA Conference on Dynamics and Control of Space Systems. IAA-AAS-DyCoSS2-14-06-02, 2014 3/24-26.
• Hongru Chen, Yasuhiro Kawakatsu and Toshiya Hanada. "Low-energy Escape from the Sun-Earth L2 Utilizing Unstable Manifolds and Lunar Gravity Assists" 24th AAS/AIAA Space Flight Mechanics Meeting. AAS 14-468, 2014 1/26-30.
• Sarli, B.V.; Kawakatsu, Y. "Orbit Transfer Optimization for Multiple Asteroid Flybys" SICE Annual Conference. TuBT7.4, 2013 9/14-17.
• Yoshihide Sugimoto, Yasuhiro Kawakatsu and Takanao Saiki. "Orbit maintenance method for orbits around Sun-Earth L2 in ER3BP" 23rd Workshop on JAXA Astrodynamics and Flight Mechanics. C-17, 2013 7/29-30.
• Yasuhiro Kawakatsu. "An orbit plan of AKATSUKI to avoid long eclipse on Venus orbit" 23rd Workshop on JAXA Astrodynamics and Flight Mechanics. B-13, 2013 7/29-30.
• Federico Zuiani, Yasuhiro Kawakatsu and Massimiliano Vasile. "Multi-objective optimisation of multi-revolution, low-thrust orbit　raising for DESTINY mission" 23rd Workshop on JAXA Astrodynamics and Flight Mechanics. B-14, 2013 7/29-30.
• Yasuhiro Kawakatsu, Kazutaka Nishiyama, Ikkoh Funaki, Takahiro Iwata. "DESTINY Mission Description and Its Value" The 29th International Symposium on Space Technology and Science (ISTS). 2013-k-47, 2013 6/2-9.
• Yoshihide Sugimoto, Stefano Campagnola, Takanao Saiki, Yasuhiro Kawakatsu. "Multi Revolution Orbit Design in Sun-Earth Elliptic Restricted 3-Body Problem" The 29th International Symposium on Space Technology and Science (ISTS). 2013-d-02, 2013 6/2-9.
• Saori Ikeda, Yoshihide Sugimoto, Yasuhiro Kawakatsu, Toshiya Hanada. "Systematic Analysis of Venus Earth Gravity Assist (VEGA) Sequence and Its Application to Mission Design" The 29th International Symposium on Space Technology and Science (ISTS). 2013-d-22, 2013 6/2-9.
• Campagnola, S., Kawakatsu, Y. Recovery options for the Akatsuki spacecraft, International Astronautical Conference, Beijing, China, Sep. 2013.

国内会議 (Selected)

• 香山裕樹,川勝康弘,"Transfer Method from Hyperbolic Orbit to Circle Orbit",第60回宇宙科学技術連合講演会,函館,9/6-9,2016.
• 川勝康弘、SPICAプリプロジェクトチーム. SPICA リスク低減 フェーズ＃２の概要. 第14回宇宙科学シンポジウム. P2-44, 2014 1/9-10.
• Yoshihide Sugimoto, Chit Hong Yam, Stefano Campagnola, Bruno Sarli, Hongru Chen, Satoshi Ogura, Yasuhiro Kawakatsu. "Preliminary Trajectory Design of An Asteroid Flyby Micro Explorer - PROCYON" 第14回宇宙科学シンポジウム. P2-122, 2014 1/9-10.
• Sugimoto, Y., Kawakatsu, Y. and Nakamiya, M. "Efficient Trajectory Correction Maneuver for Low Energy Transfer Trajectory to Halo Orbits" The 30th SICE Guidance, Navigation, and Control Symposium. 1L4-2, 2013 5/16-17.